
Mathematics
Explore the art of logic and problem solving.
Develop a Sought-After Quantitative Skill Set
Core Ideas and Collaboration
Oberlin Mathematics Professor Jack Calcut helps students grasp the core ideas behind a proof before translating those ideas into mathematical language.

Creativity and Structure
Math students learn to combine imagination with logic. In Professor Bob Bosch’s seminar students make the connection literal, using mathematics to create art.

Featured Courses
Cryptography
Explore the science of making and breaking secret codes. We start with codes that Julius Caesar would have used in his armies. To make more sophisticated codes, we need to learn about a branch of mathematics called number theory. These tools will help us understand the modern cryptosystems (like RSA) that the internet is built on.
- Taught by
- Benjamin Linowitz
Discrete Mathematics
Mathematics is a language, and this class teaches you to “speak math.” We introduce topics you will not have seen in calculus (such as logic, sets, induction, number theory, combinatorics, graph theory) and emphasize creative problem solving and proof writing. At the end, you will be prepared to tackle many of our upper level offerings.
- Taught by
- Jack Calcut
Probability
Dealing with uncertainty is critical in many applications of mathematics. For example, it is important in machine learning, statistical modeling, economics, actuarial science, and physics. This class uses the tools you’ve learned in 200 level classes to give uncertainty and probability a firm mathematical foundation, ready to be applied to other fields.
- Taught by
- Elizabeth Wilmer
Harmonic Analysis
Ever since the imperfections of Pythagorean tuning gave evidence for the existence of irrational numbers, music has inspired important developments in mathematics. We start with these classical results and work our way towards modern methods like the Fourier transform, with its applications to acoustics.
- Taught by
- Chris Marx
Student Profiles
The Course that Changed Everything
Alina Zhu always loved how math could be used to untangle musical principles. It could further a career. It was, she thought, a useful tool. But in the fall of her sophomore year, she took a math course that changed her entire perspective on the field.
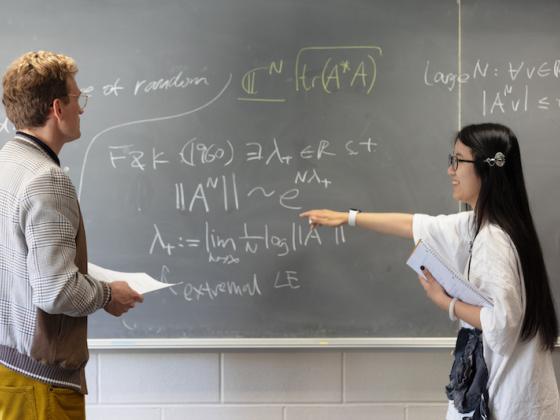
Particle Systems as Epidemics
Mathematics major Garrett Robins has been researching the behavior of particle systems to model the diffusion of disease and opinion.

The Future of Sustainable Buildings
Math and physics double major Grant Sheely was also captain of Oberlin’s cross country and track and field teams. He went on to work as a sustainability coordinator in New York City.

Upcoming Mathematics Events
Mathematics Department Open House
What does mathematics at Oberlin look like?

Professor Bob Bosch explaining his research at the intersection of mathematical optimization and art.

Professor Elizabeth Wilmer helping students with a homework problem in King 203, our library and math major lounge.

Students celebrating Pi Day. With homemade pies!

Four Oberlin students making an "N" after virtually attending the "N"ebraska Conference for Undergraduate Women in Mathematics.
